이번에는 matrix factorization과 유사성 측정에 대해 알아보겠다.

Matrix factorization

먼저, Wikipedia에서의 Matrix factorization이다.

Non-negative matrix factorization

Non-negative matrix factorization (NMF or NNMF), also non-negative matrix approximation is a group of algorithms in multivariate analysis and linear algebra where a matrix V is factorized into (usually) two matrices W and H, with the property that all three matrices have no negative elements.

Non-negative matrix factorization

요약해서, W와 H의 두 matrix의 곱으로 V matrix를 분해하여 저장한다. 그렇게 되면 속성 간의 연결성을 파악할 수 있다는 것이다.

예를들어, 다음 matrix A가 있다.

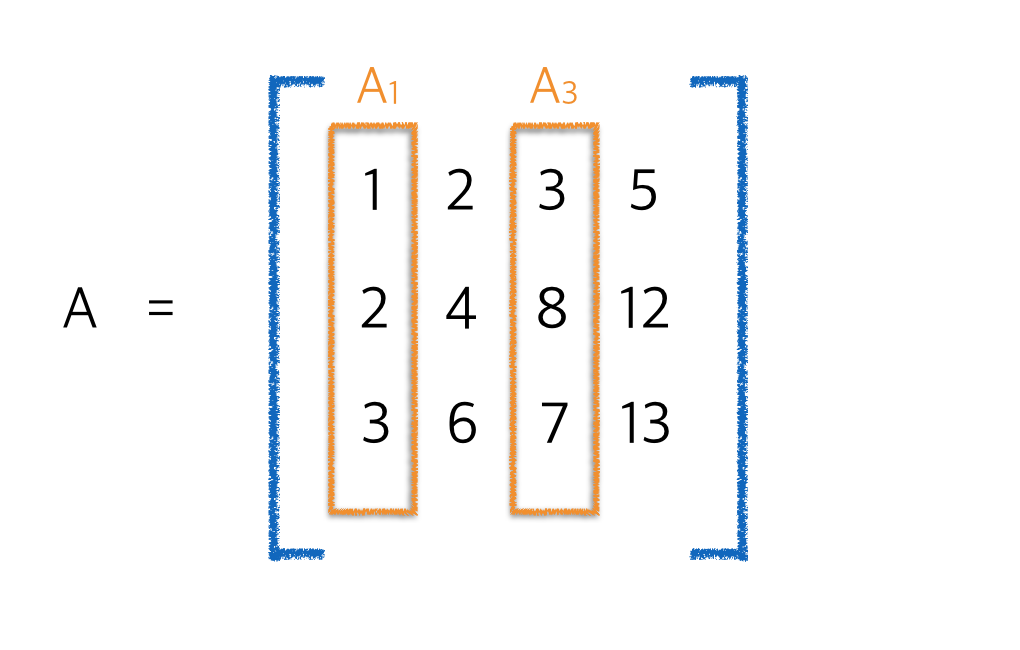
Matrix A

이 matrix의 첫번째 열부터 A1, 마지막(네번째) 열을 A4라 하자. 이 중에서 A1과 A3를 기준으로 다음과 같은 특징을 뽑을 수 있다.

A1 = 1 * A1 + 0 * A3
A2 = 2 * A1 + 0 * A3
A3 = 0 * A1 + 1 * A3
A4 = 2 * A1 + 1 * A3

따라서 A1과 A3의 행렬곱으로 나누면 다음과 같이 나눌 수 있다.

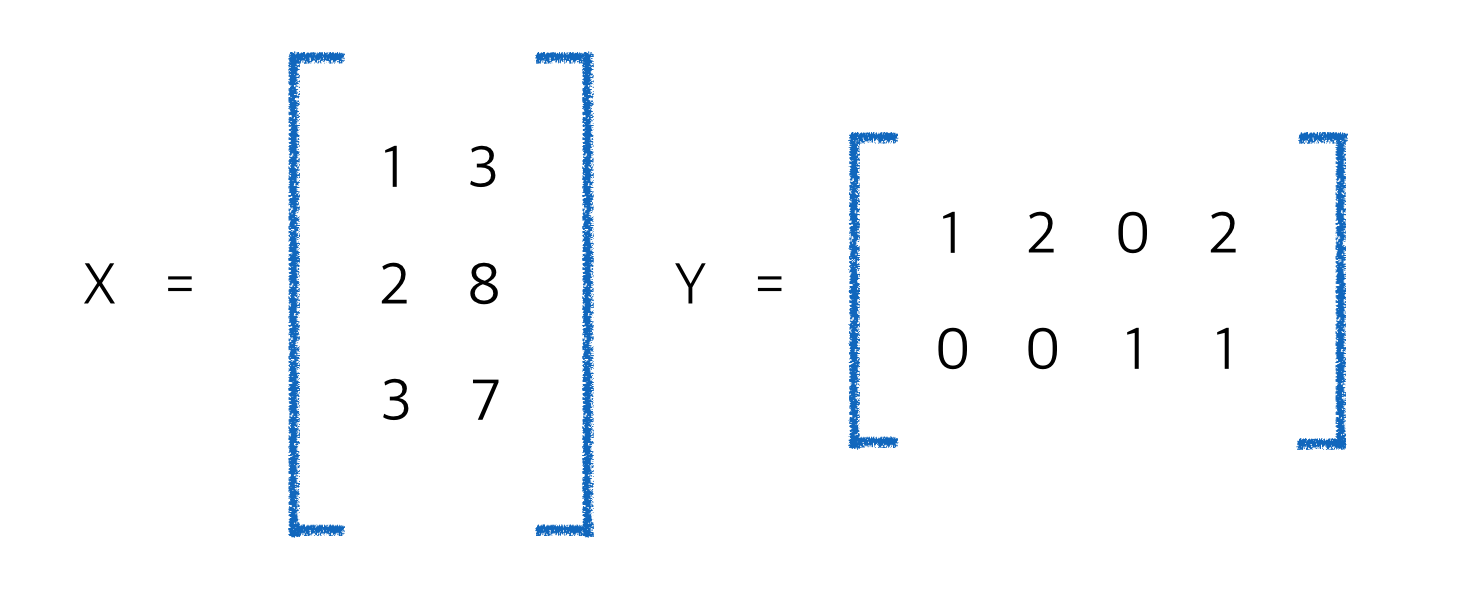
Matrix X & Y

이를 다시 곱하면 다시 Matrix A가 나오는 것을 검산도 가능하다. 이와 같이 특정한 행렬에서 속성을 추출하기 위해 사용되는 것이 matrix factorization이며, 이는 특정 사용자 간의, 혹은 특정 아이템 소비군들의 유사도를 분석하는데 큰 도움이 된다.

유사성 측정

유사성 측정에는 유클리드 거리, 코사인 유사도, 피어슨 상관계수를 활용한다.

유클리드 거리

유클리드 거리는 두 점 사이의 거리를 계산하기 위한 공식이다.

Euclidean distance

코사인 유사도

코사인 유사도는 내적공간의 두 벡터 간 각도의 코사인 값을 이용해 측정된 벡터 간의 유사한 정도를 의미한다. 벡터의 크기가 아니라 방향의 유사도를 판단하는데 주 목적이 있다.

Cosine Similarity

피어슨 상관계수

피어슨 상관계수는 두 변수간의 관련성을 구하기 위해 보편적으로 사용된다

Pearson correlation coefficient

이를 이용해 matrix factorization을 이용한 특정 행에 대한 임의의 행렬A와 B의 곱을 구하고, 그에 대한 유사도를 측정한다.